Le Reti Neurali Convoluzionali, ovvero come insegnare alle macchine a riconoscere per astrazione
Le Reti Neurali Convoluzionali, o ConvNet (CNN) sono uno degli algoritmi di Deep Learning più utilizzati oggi nella computer vision e trovano applicazione in tantissimi campi: dalle automobili autonome ai droni, dalle diagnosi mediche al supporto e trattamento per gli ipovedenti.
Cos’è una convoluzione?
Wolfram Alpha la spiega così:
A convolution is an integral that expresses the amount of overlap of one function
as it is shifted over another function
. It therefore “blends” one function with another. For example, in synthesis imaging, the measured dirty map is a convolution of the “true” CLEAN map with the dirty beam (the Fourier transform of the sampling distribution).
Matematicamente parlando, la parola “convoluzione” significa “far scorrere” una funzione (blu) sopra un’altra (rossa), di fatto “mescolandole” assieme. Il risultato sarà una funzione (verde) che rappresenta il prodotto delle due funzioni.

La curva verde mostra la convoluzione delle curve blu e rosse in funzione di t. La regione scura in funzione di t è precisamente la convoluzione.
Convoluzioni applicate alle reti neurali
Questa è una definizione rigorosamente matematica del processo, ma in che modo ci interessa?
Nel caso ad esempio dell’analisi di immagini, la funzione rossa rappresenta l’immagine analizzata in input, mentre la seconda (blu) è conosciuta come “filtro”, perché identifica un particolare segnale o struttura nell’immagine.
In parole più semplici, analizzando un’immagine, un primo stadio potrebbe essere quello di riconoscere le silouette delle figure. Quindi, semplificando, ci troveremmo ad esempio un filtro per le linee verticali, uno per le orizzontali, uno per le diagonali, tutti e tre che “passano” sull’intera immagine.
Layer successivi potrebbero per esempio riconoscere occhi, orecchie, mani, etc. Alla fine, l’ultimo layer potrebbe essere in grado di riconoscere e distinguere pecore, persone, automobili.
Perché inventare le convoluzioni?
Innanzitutto vale la pena capire perché inventarsi algoritmi tutto sommato complessi come le convoluzioni: non sarebbe meglio avere una rete fully connected? In fin dei conti con una rete fully connected non c’è perdita di informazioni. Il problema è che una rete totalmente fully connected porta a un’esplosione combinatoria del numero di nodi e connessioni richieste1.

Rete neurale fully connected. Ogni nodo è collegato con tutti i nodi dei layer precedente e successivo
Reti neurali convoluzionali e filtri
Le reti neurali convoluzionali funzionano come tutte le reti neurali: un layer di input, uno o più layer nascosti, che effettuano calcoli tramite funzioni di attivazione, e un layer di output con il risultato. La differenza sono appunto le convoluzioni.
Ogni layer ospita quella che viene chiamata “feature map”, ovvero la specifica feature che i nodi si preoccupano di cercare. Nell’esempio qui sotto il primo layer potrebbe occuparsi di codificare le linee diagonali, quindi si “fa scorrere” un apposito filtro (qui nell’esempio un 2×2) sull’immagine, e moltiplicandolo (prodotto scalare) per l’area sottostante.
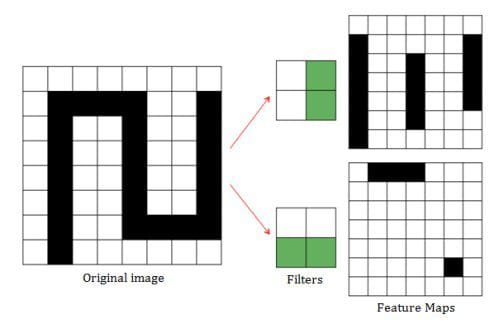
Feature maps generate da filtri per linee verticali e orizzontali
Questa moltiplicazione corrisponde alla funzione che abbiamo visto all’inizio dell’articolo, dove l’immagine di input corrisponde alla curva rossa, il filtro alla blu, e la feature map alla verde. In sostanza significa che all’interno del layer convoluzionale ciascun nodo è mappato solo su un sottoinsieme di nodi di input (campo recettivo), e di fatto moltiplicare il filtro per il campo recettivo di ciascun nodo equivale concettualmente a “far scorrere” il filtro lungo l’immagine di input (windowing).

Processo di windowing
L’ Architettura delle reti neurali convoluzionali
Il risultato sarà un’altra matrice, leggermente più piccola dell’immagine originale, o della stessa grandezza se si usa zero padding2, chiamata appunto feature map. Ad ogni layer di neuroni si possono applicare eventualmente più filtri, generando quindi più feature map.

Rete Neurale Convoluzionale: architettura
Tipicamente ogni layer convoluzionale viene fatto seguire da uno di Max-Pooling3, riducendo via via la dimensione della matrice, ma aumentando il livello di “astrazione”. Si passa quindi da filtri elementari, come appunto linee verticali e orizzontali, a filtri via via più sofisticati, in grado ad esempio di riconoscere i fanali, il parabrezza… fino all’ultimo livello dove è in grado di distinguere un’automobile da un camion.
Note
1 Giusto per darci un’idea, un’immagine a colori piccolissima 32×32 pixel, porterebbe ad avere nel primo layer già 3072 nodi (32×32 pixel x 3 canali di colore), con 3072 connessioni ciascuno (più di 9 milioni totali). Un’immagine di dimensioni più ragionevoli 1000×1000 porterebbe ad avere 1M di nodi con 1m di connessioni ciascuno, ovvero un totale di 10^12 connessioni! È quindi evidente che una soluzione di questo tipo non è scalabile e totalmente irrealistica.
2 Zero padding è una tecnica che consiste nell’aggiungere (vedi sotto) all’immagine un “bordo” di zeri (vedi sotto), allo scopo di preservare la dimensione dell’immagine in uscita dal layer, per non perdere informazioni.
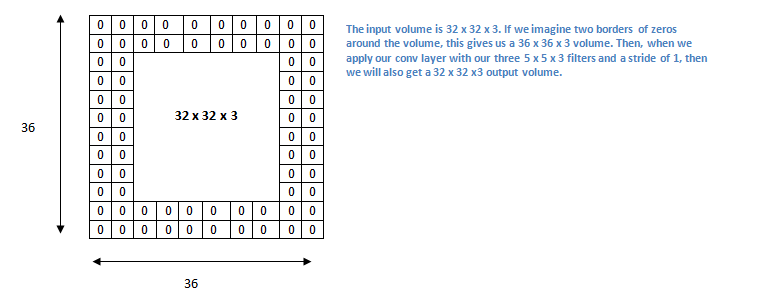
3 Il max-pooling è un metodo per ridurre la dimensione di un’immagine, suddividendola in blocchi e tenendo solo quello col valore più alto. Così facendo si riduce il problema di overfitting e si mantengono solo le aree con maggiore attivazione.

LINK
An Intuitive Explanation of Convolutional Neural Networks
A Beginner’s Guide to Deep Convolutional Neural Networks (CNNs)
Convolutional Neural Networks (CNNs / ConvNets)
The best explanation of Convolutional Neural Networks on the Internet!





